A recent MarketWatch piece cited a talk in Hong Kong by Economics Nobel Prize winner Professor Robert Merton wherein he discussed the challenges of evaluating investment managers. The following article assumes that the above summary of Professor Merton’s talk is accurate. The piece, and assumedly the talk, argued that, given typical nominal portfolio returns and volatilities, it takes impractically long to detect evidence of investment skill. The argument claimed to prove that all manager selection is futile. Instead, it proved that naïve nominal performance metrics are of little use.
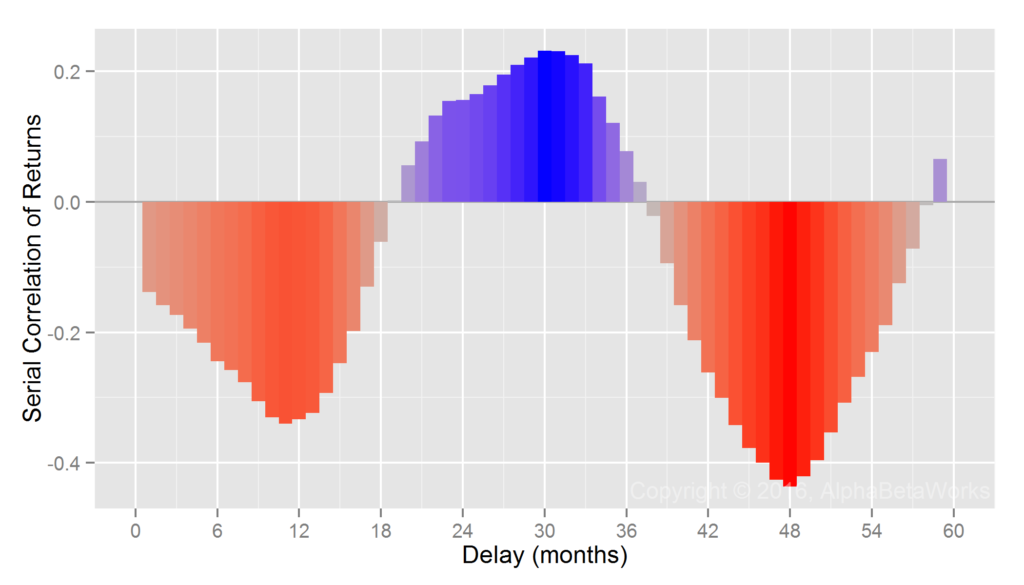
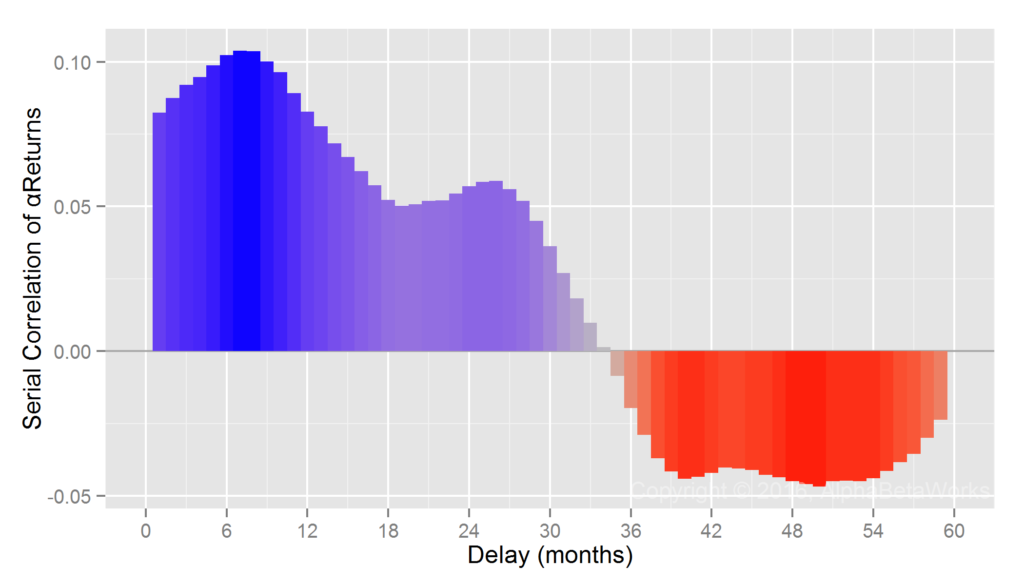
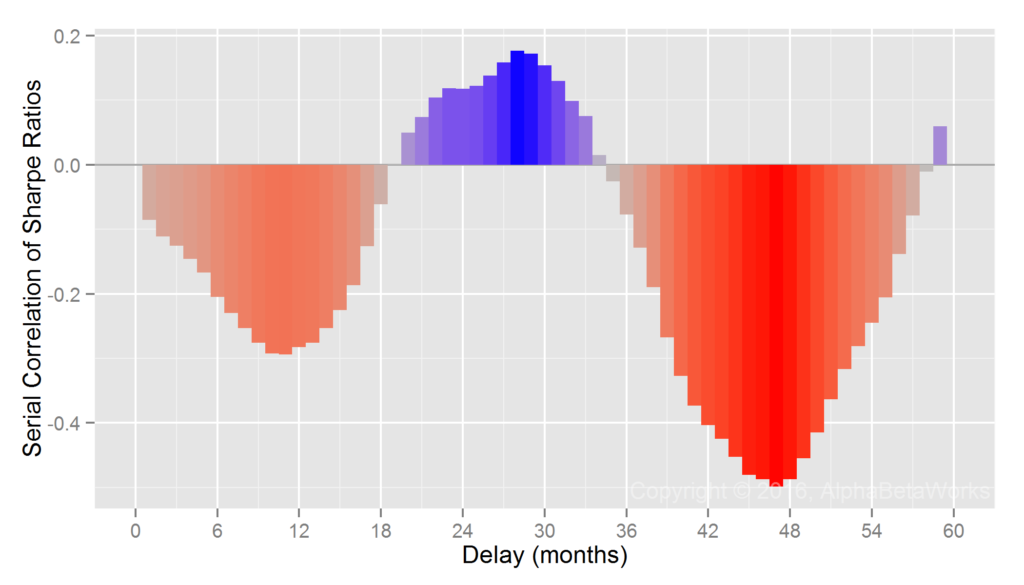
Any test of the effectiveness of manager selection is also a test of the analytical process that distills skill. That nominal investment performance is primarily due to factor (systematic, market) noise and thus reverts is well-known. It is thus unsurprising to find flaws in an approach to manager selection that is as antiquated as Ptolemaic Astronomy.
In this article, we will illustrate the difference between a naïve attempt to detect evidence of investment skill using nominal returns and a more productive effort relying on alphas (residual, security selection, stock picking returns) isolated using a capable modern multi-factor equity risk model. Whereas the former approach is futile at best, the latter approach is successful. In fact, rather than taking decades, a capable modern system can identify skill with high confidence in months.
Detecting Evidence of Investment Skill Using Nominal Returns
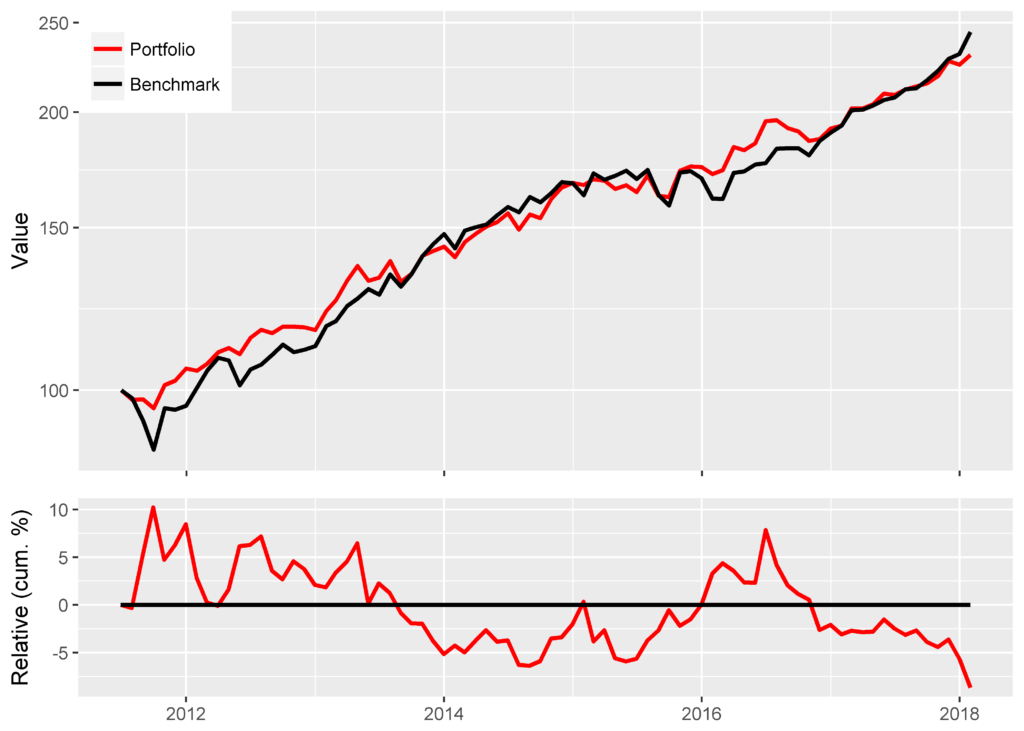
Consider nominal returns of a Portfolio and a Benchmark. The Portfolio is a live long-only fund implementing a Smart Beta active investment strategy:
Portfolio Benchmark Annualized Return 0.1336 0.1433 Annualized Std Dev 0.0879 0.1093 Annualized Sharpe (Rf=0%) 1.5194 1.3115
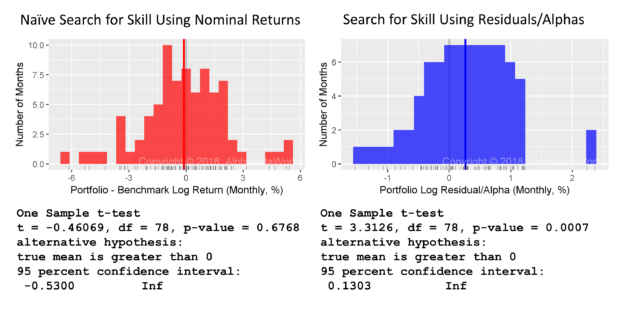
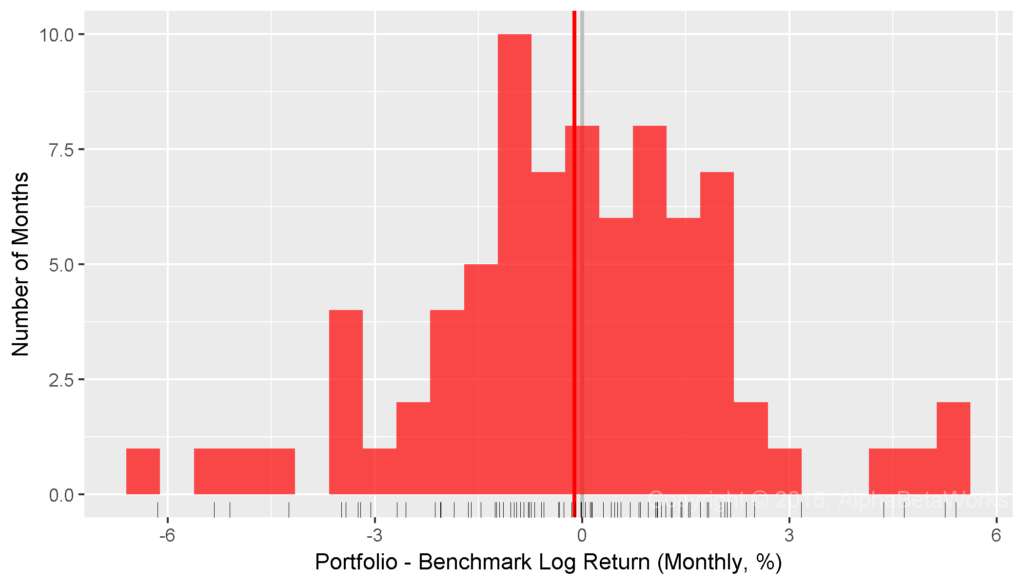
With a heroic assumption that log returns follow a normal distribution, a t-test appears to confirm Professor Merton’s argument. Even with over six years of data, the returns are too noisy for a statistical inference:
Min. 1st Qu. Median Mean 3rd Qu. Max. -6.1441 -1.2186 -0.0201 -0.1149 1.2481 5.4068 One Sample t-test t = -0.4607, df = 78, p-value = 0.6768 alternative hypothesis: true mean is greater than 0 95 percent confidence interval: -0.5300 Inf
Detecting Evidence of Investment Skill Using Alphas/Residuals
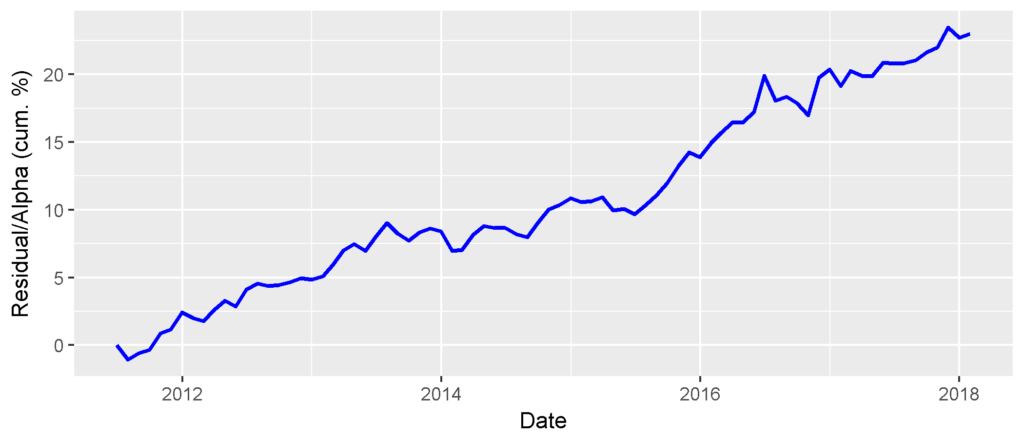
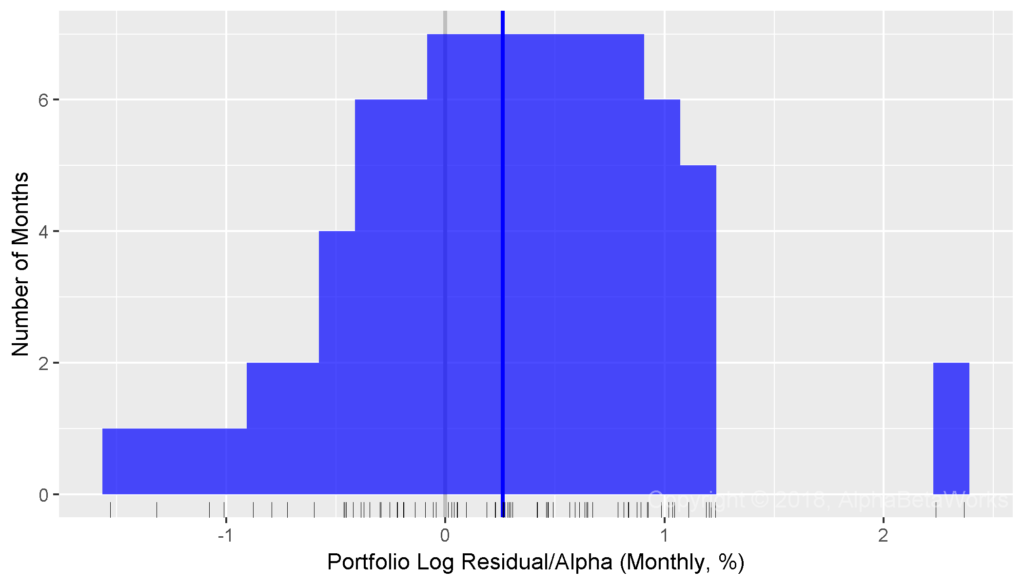
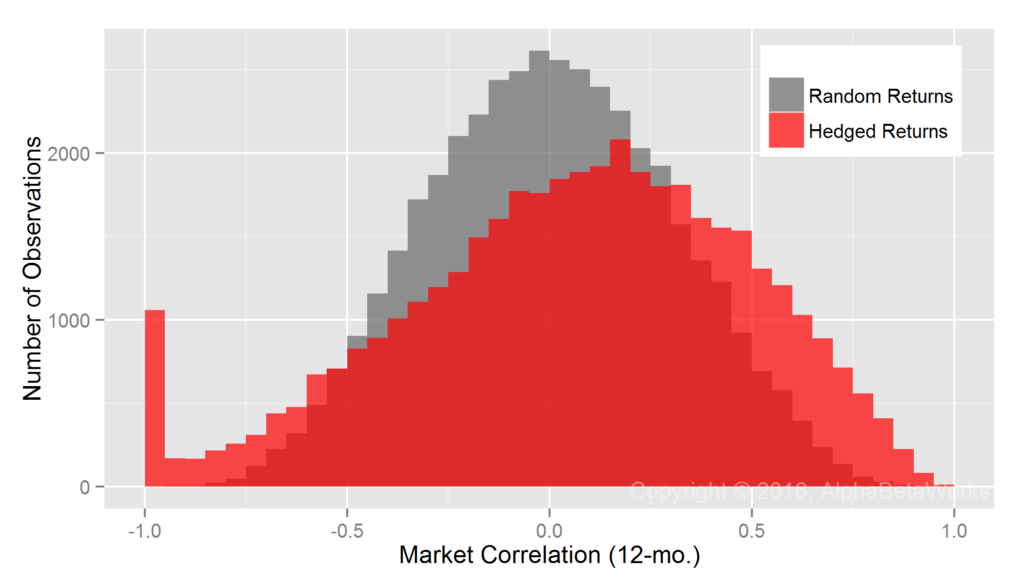
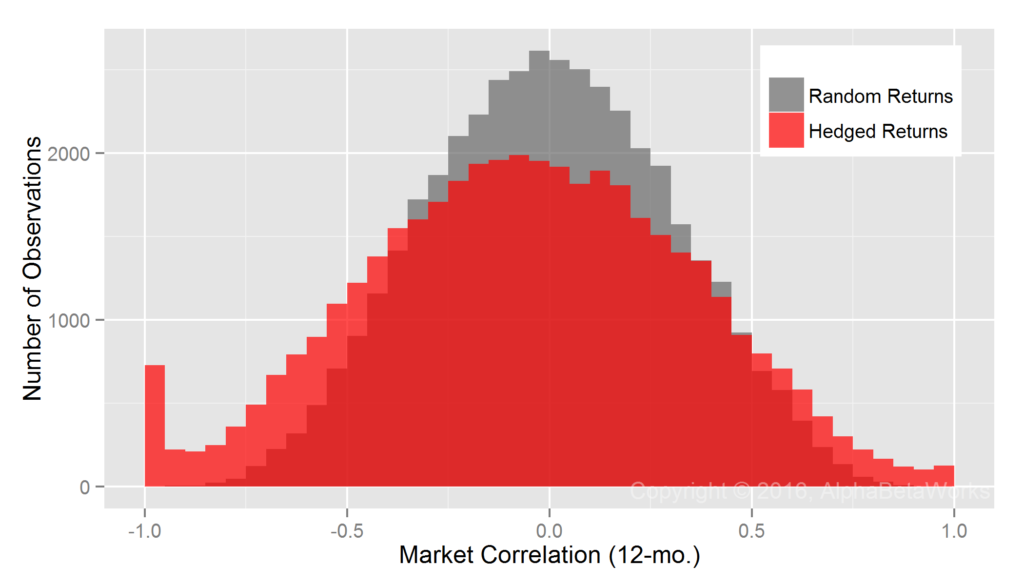
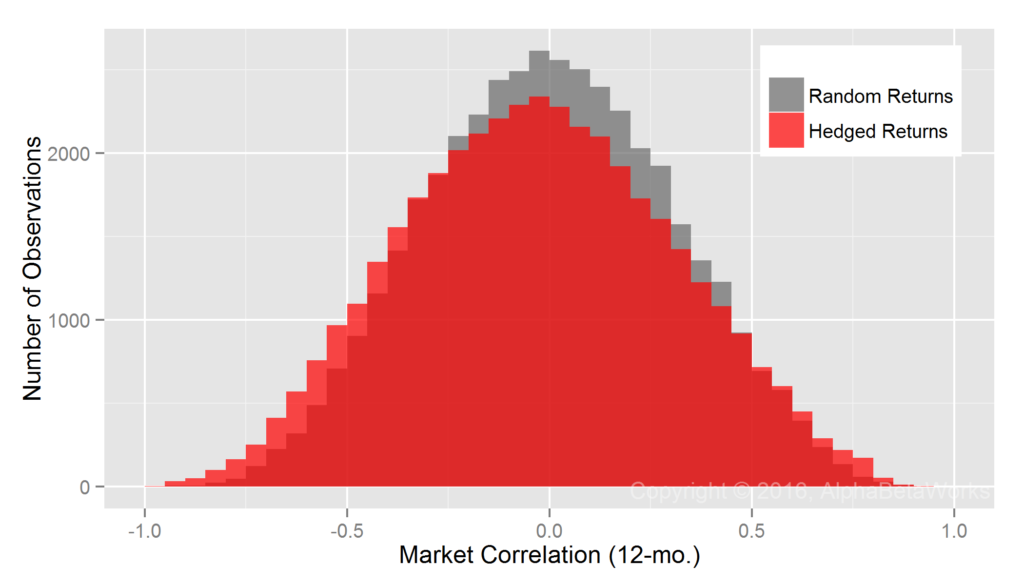
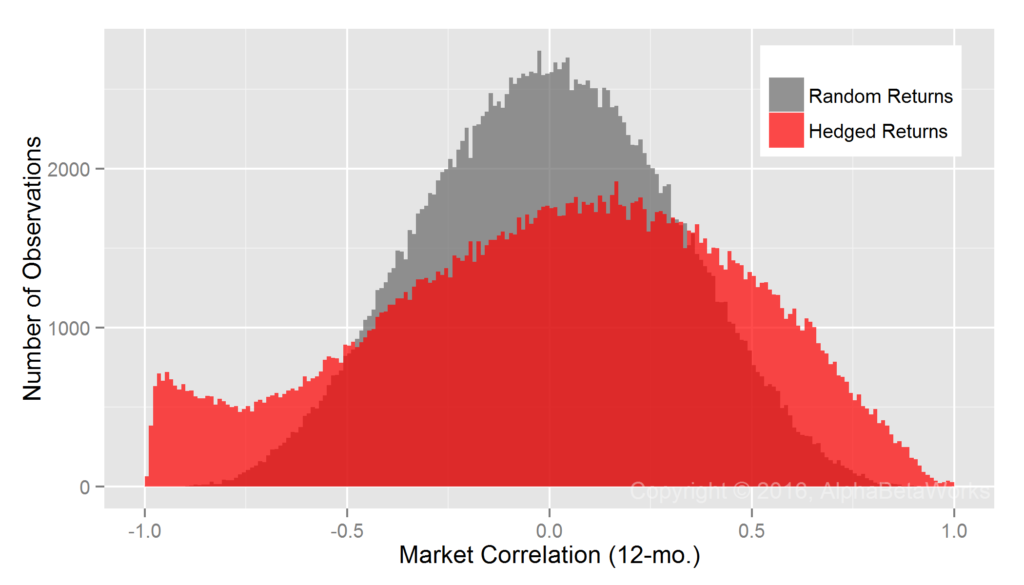
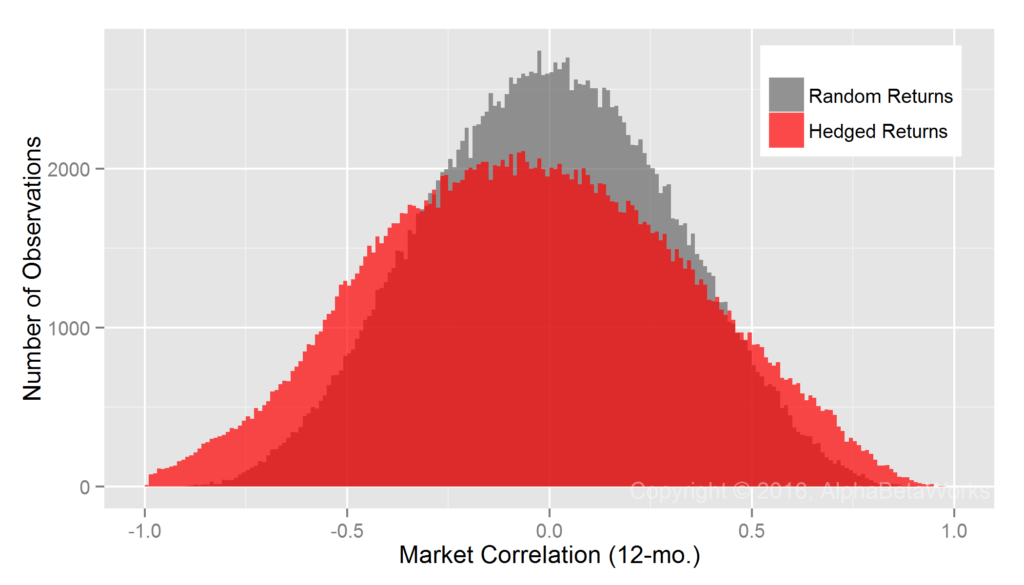
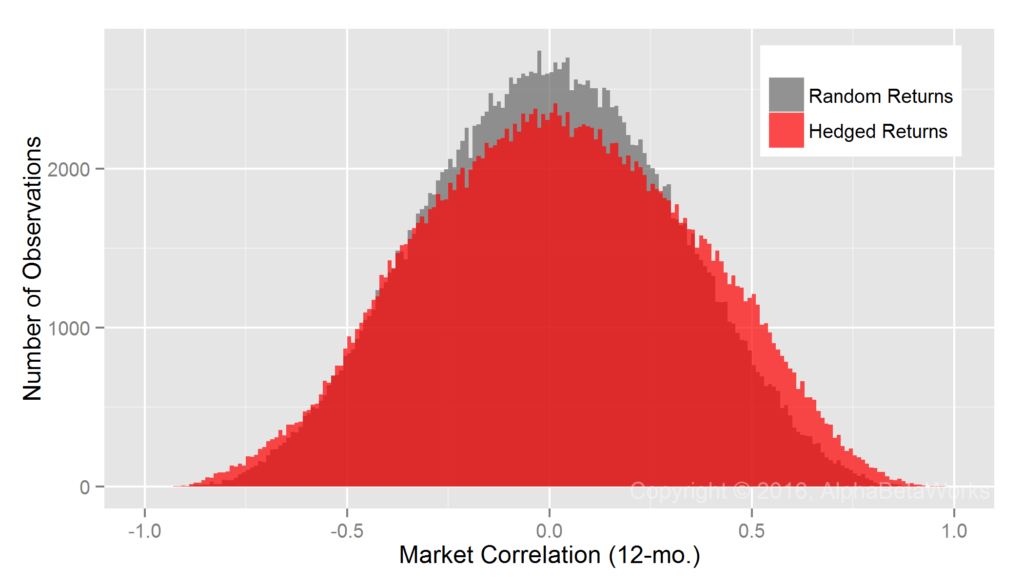
By comparison, consider the same Portfolio’s residual returns, or alphas, for the same period, isolated with the AlphaBetaWorks’ standard Long-Horizon Statistical U.S. Equity Risk Model. These are also the returns Portfolio would have generated if its factor exposures had been fully hedged (its returns factor-neutralized, or residualized) using the Model:
With an equally questionable assumption that log residuals follow a normal distribution, a t-test is now highly statistically significant:
Min. 1st Qu. Median Mean 3rd Qu. Max. -1.5300 -0.2064 0.2643 0.2620 0.7289 2.3663 One Sample t-test t = 3.3126, df = 78, p-value = 0.0007 alternative hypothesis: true mean is greater than 0 95 percent confidence interval: 0.1303 Inf
Whereas Professor Merton’s argument does indeed apply to nominal returns, it does not apply to their residuals. A critical difference is the lower dispersion of residual returns. Over 90% of the variance of a typical active equity portfolio is due to factor exposures rather than to stock picking. Therefore, using nominal returns to measure skill is like trying to take a baby’s temperature by examining her bath water, rather than the baby herself.
Whereas at least 67 out of 100 monkeys picking stocks at random are expected to outperform the Portfolio, less than 1 out of 1,000 is expected to generate higher residuals – a highly statistically significant result. Thus, with the help of a capable equity risk model, strong evidence of skill can be identified in months rather than in decades.
Converting Residuals into Nominal Outperformance
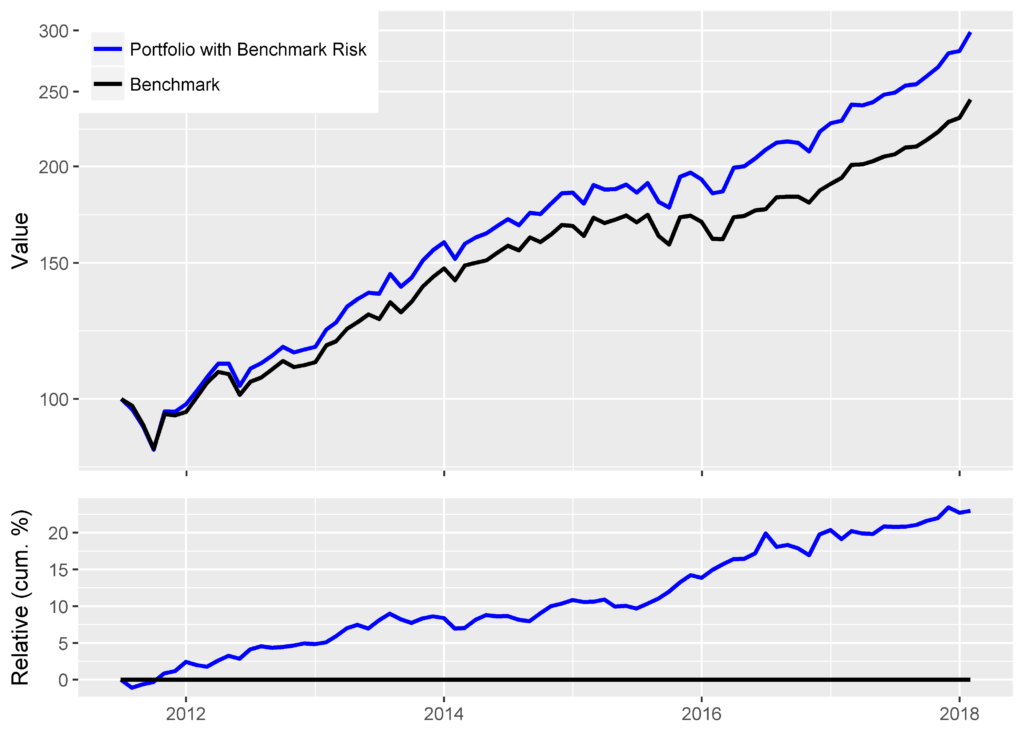
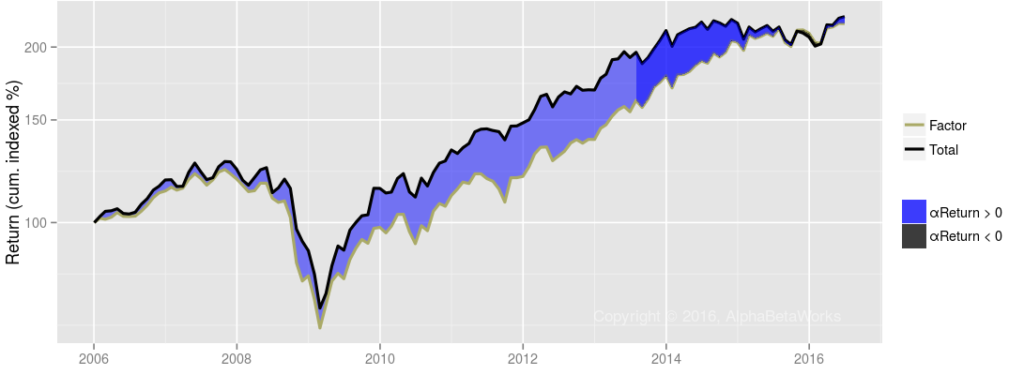
Assuming the equity risk model uses investable factors, as AlphaBetaWorks’s models do, the residual return stream above is investable. In fact, in the idealized case of costless leverage, positive residual returns can be turned into outperformance relative to any benchmark. Below is the performance of Portfolio after it is hedged to match the factor exposures of the Benchmark. The evidence of skill is now plainly visible in the naïve absolute and relative nominal return metrics:
Portfolio with Benchmark Risk Benchmark Annualized Return 0.1784 0.1433 Annualized Std Dev 0.1168 0.1093 Annualized Sharpe (Rf=0%) 1.5276 1.3115
Conclusions
- Since factor noise dominates nominal returns, the use of nominal returns to detect evidence of investment skill takes far too long to be practical.
- After distilling stock picking performance (alphas, residual returns) from factor noise, statistically significant evidence of investment skill can become evident in months, rather than in decades.
- Hedging makes it possible to turn positive stock picking returns into nominal outperformance with respect to any benchmark.